
三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ
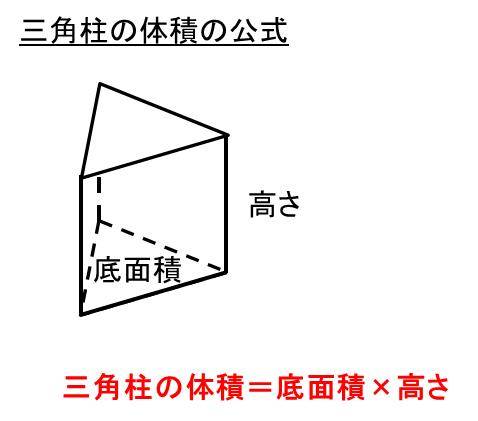
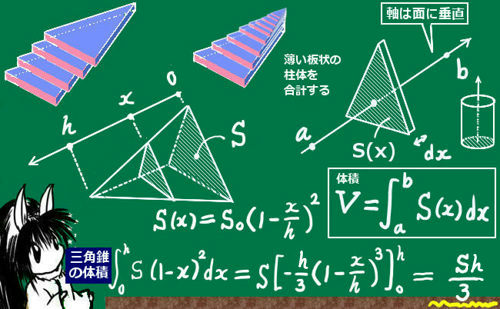
三角錐の体積=100×10÷3=3333cm 3 です。 三角錐の体積と底面積の関係 三角錐の体積は下式でも算定できます。 三角錐の体積=三角錐の底面積×三角錐の高さ÷3 三角錐の底面積とは、「三角形の面積」と同じです。同様に、三角柱の体積=底面積×三角柱の高さです。三角形の面積は下記も参考にな 角錐の体積はなぜ底面積×高さを3で割るのか 04年1月10日 入社試験で「正四面体の体積を求よ」というのを出題したことを書いたことがある。 結果はさんざんだったのだが、さらに気になったことが出てきた。
三角錐 体積 求め方 中学生
三角錐 体積 求め方 中学生- 12三角錐の体積公式 錐の体積 底面積×高さ× (1/3) 三角錐に限らず、錐の体積を求めるには柱との関係で捉えるとよいでしょう。 つまり、柱の体積に3分の1をかければ、錐の体積が求まるという関係にあります。 そして、これを三角錐に関して表現すると、 三角錐の体積 底面積(三角形の面積)×高さ× (1/3) このように表現されることになります。〇 三角錐の体積は、底面積を求めて高さをかける、そして\(\times \frac{1}{3}\)を忘れないように! 三角錐の表面積 三角錐の表面積を問われることは少ないようですが、難しい話ではないのでサクッと解説しておきますね。 まずは三角錐の展開図がどんなものか確認しておきましょう。 底面の

三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
≪三角すいEABDの体積≫ 1 3 ×{(12×12÷2)×12} =2 ※同じ形が全部で4個(EABD、BFGE、GCBD、DHEG) 2×4 =1152 ≪立方体の体積-三角すい4つのの体積≫ 1728-1152 =576 ≪答≫ 体積:576cm 3 2 右の立方体を、2点F,Hと、辺BC上の点P、辺CDの点Qを通る 平面で2つに分ける。 (CP=CQ=4cm) このとき、点Gをふくむ側の立体の体積を答えなさい。 ≪ x を求める≫ x : (四角錐の表面積=底面積 側面積(三角形 つ分) では、実際に問題を解いてみましょう。 次の四角錐の表面積を求めなさい。 (底面は正方形) 展開図を書いて、側面積と底面積を求めると次のようになります。 同じ三角形が4つ分集まって側面になっているので、1つ分の三角形の面積を求めて4倍すると側面積を求めることができますね。 これは底面が正方形 この、中にある三角錐の体積の求め方が分かりません。 解説お願いします。 3右の図は, 1辺の長さが5cmの立方体で, 図のように AP=1cm, 30 360 BQ=3 cm, CR=D2 cm となる点 P, Q, Rを立方体の辺上にとる。 こ の立方体から, 4点 B, P, Q, Rを頂点とする三角錐を切り取るとき, 残りの立体の体積を求めなさい。 D A R H G E F 立体の体積 回答 ベストアンサー 私立文系 (指定校) 約1年前 三
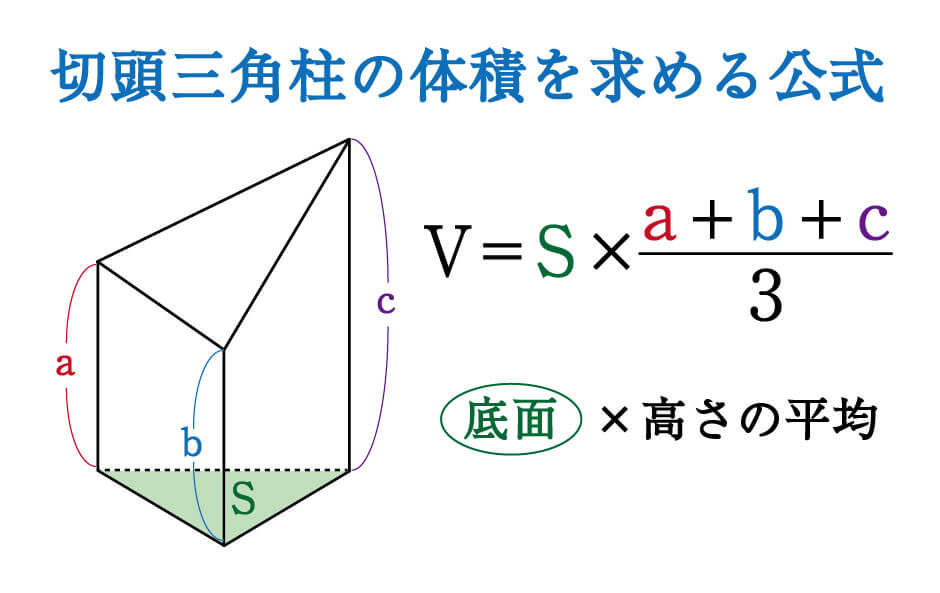
一般に、球の体積は、その球がすっぽり入る円柱の体積の \(\frac{2}{3}\) となります。 ここから \begin{eqnarray} \mbox{球の体積} &=& \frac{2}{3} \times \mbox{すっぽりな柱の体積} \\ &=& \frac{2}{3} \times \ r \times r \times \pi \times 2r \\&=& \frac{2}{3} \times 2 \pi r^3 \\ &=& \frac{4}{3} \pi r^3 \end{eqnarray} 三角柱の高さ=三角柱の体積÷底面積であることから 求める三角柱の高さ=168÷(12×7÷2)=4(cm) 別解 もともとの三角柱の高さ=三角柱の体積÷底面積=504÷(12×7÷2)=12(cm) 求める三角柱の高さは、もともとの三角柱の高さの3分の1であることから 求める三角柱の高さ=12(cm)÷3=4(cm)となります。 答え 4cm ~立体の体積・表送信を完了しました。 角錐台の体積 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に役に
三角錐 体積 求め方 中学生のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三角錐 体積 求め方 中学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
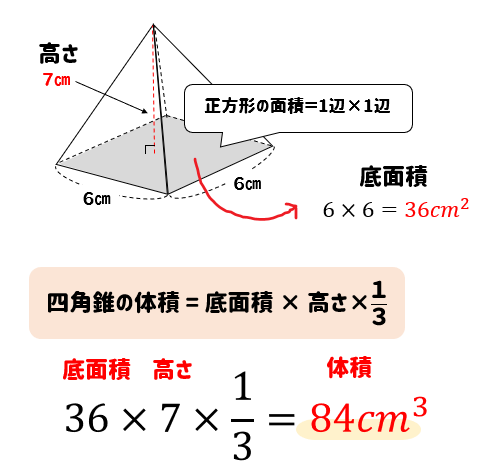
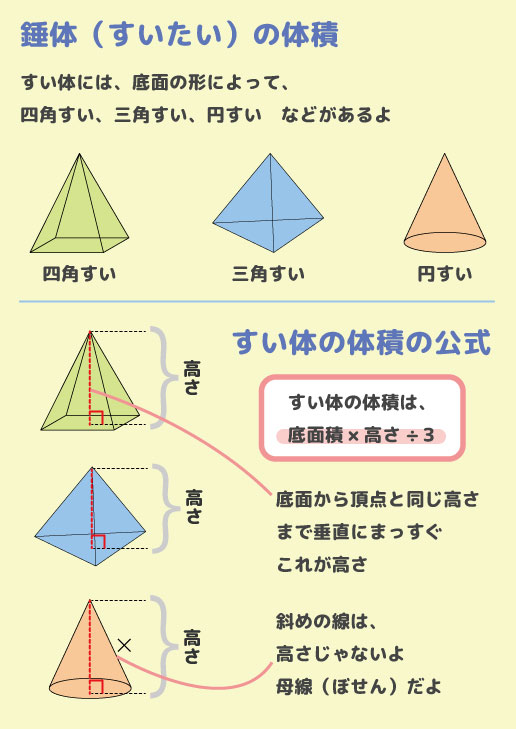
V =(3 * H /√6)³*√2/12 = 27 *√2 * H 3 /(12 *(√6)³ ) これらすべての根と次数を取り除くには、それらをの小数桁数に置き換えます。 V =H³* 。 6 正三角錐が既知の半径(R)の球に内接すると、体積(V)の計算式は次のように書くことができます。 V = 16 *√2 * R 3 /(3 *(√6)3)。 実際の計算では、すべてのべき乗式を十分な精度の小数点以下1桁で置き換え「すい」 の体積は注意しよう。 (底面積)×(高さ)×1/3 この 1/3 を忘れてしまってはダメだよ。
Incoming Term: 三角錐 体積 求め方 中学生,




0 件のコメント:
コメントを投稿